鶴亀算 つるかめ算 算数文章問題の鶴亀算(つるかめ算)とは、 例えば、鶴と亀の合計の数と、その足の合計の本数が分かっているとき、鶴と亀のそれぞれの数を求めるような問題を鶴亀算といいます。 「例題」 鶴・亀あわせて、頭数は10、足の数は32本書に鶴亀算が取り上げられていることがわかったので鶴亀算の歴史について改めて調べてみた。既存 の書籍からの転載ではなくインターネットを利用して、できるだけ原典を調べるように努めた。 2.中国の算術書より 孫子算経→算学啓蒙→算法統宗 中学入試まんが攻略bon!(算数 つるかめ算)新装版 学研教育出版 本の購入は楽天ブックスで。全品送料無料!購入毎に「楽天ポイント」が貯まってお得!みんなのレビュー・感想も
Http Www2 Ttcn Ne Jp Nagai Waseda Wasan Turu Pdf
鶴亀算 歴史
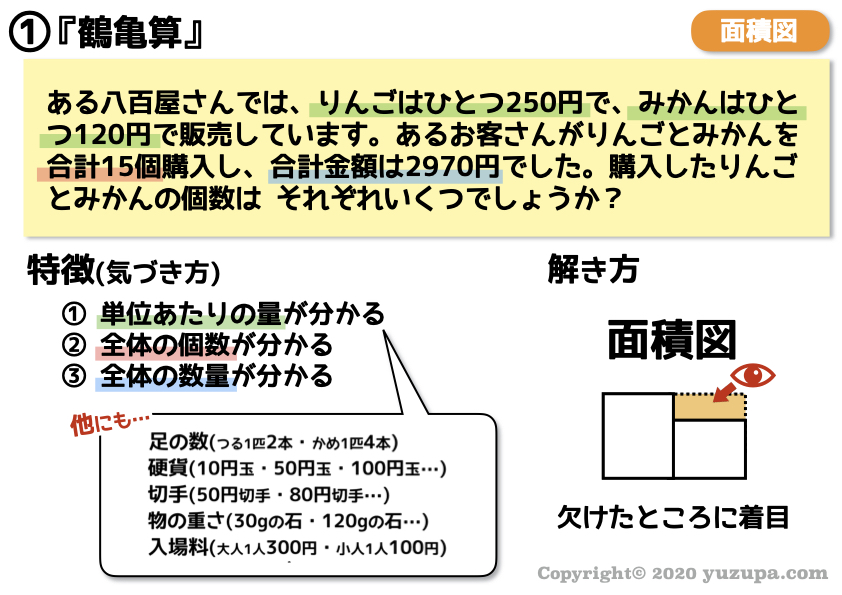
鶴亀算 歴史- 以上、『『鶴亀算』たった2種類の公式と解き方のコツ』を紹介しました。 図解すると解りやすいですね。 しかし試験問題にはツルの数とカメの数は出てきません。 リンゴの値段とみかんの値段と合計数からリンゴの個数とみかんの個数を求めるような鶴亀算って何の役に立つの? 鶴亀算が苦手という人のために気楽に読んで学べる鶴亀算に関するお話を用意しました。 考え方、解き方のヒントとなることが見つかるかもしれません。 勉強していて、 これって何の役に立つのだろう と思うことは多いです



Http Www2 Ttcn Ne Jp Nagai Waseda Wasan Turu Pdf
精選版 日本国語大辞典 鶴亀算の用語解説 〘名〙 算数応用問題の一つ。鶴と亀を合わせた数とその足の和を与えて、鶴と亀のおのおのの数を求める類の問題。※抒情歌(1932)〈川端康成〉「応用問題の鶴亀算なんかも、直ぐに答へを出しました」 江戸時代からあった「つるかめ算の面積図」 「つるかめ算の面積図」を歴史上初めて示したのは、関孝和の高弟の建部賢弘でしょう。 中国の『算学啓蒙』(元代1299年頃)に注解を付した『算学啓蒙諺解大成』(1690年)の「鶏と兎が100、足の数は272」という問題に付した図です。 江戸時代後期には、千葉胤秀が、『算法新書』( 10年)の中で、途中の計算の経過も鶴亀算の歴史は、4世紀の中国まで遡り、当時は鶏( または雉 )と兎だった のが、日本に 伝わっておめでたい鶴と亀に替わったそうです。 明治以降、学校教育に西洋数学が採用され、鶴亀算のような<
つるかめ算の歴史 つるかめ算は、 中国で1700年近く前(南北朝時代)に書かれたと言われている『孫氏算経』で定着しました。 しかし、ここで登場したのは「ツルとカメ」ではなく「キジとウサギ」だったのです! その約1000年後(元の時代)には「ニワトリとウサギ」に変わり、 江戸時代の日本で「ツルとカメ」に置き換えられて今に至ります。 この鶴亀算の源流 (じとどうりゅう きじとウサギが同じ篭) 雉兎同籠の問題は重要な算数の応用問題で、近代的な生活の中でどこにも見られます。 通常問題の中ではキジやニワトリではなく、ましてキジとウサギを同一のかごに閉じ込めることはありえません。 なぜ,どうしてそれを『キジとウサギが同じ篭』の問題というのでしょう。 この名前は、古くから 新連載企画「小学生でもわかる塵劫記」の第3回目です。 第1回「俵杉算」 第2回「入れ子算」 第3回は「からす算」というものを扱います。 からす算(単なる3つのかけ算
歴史 編集 中国 の数学書『 孫子算経 』にある、「雉兎同籠」が始まりとされる。 それが 江戸時代 におめでたい動物とされる ツル と カメ に置き換えられて、この名前になった。鶴亀算とは鶴と亀を例に出した計算問題のことをいいます。内容は下記 鶴と亀が合計で32匹います。 足の数をすべて足すと本になります。 鶴、亀はそれぞれ何匹ずついるでしょうか。 ただし、鶴の足は2本、亀の足は4本とします。 というような問題です。 みんなの知ってる「鶴亀算」は和算だった!? 中学受験をする小学生が塾などで習う数学に『 鶴亀算 』と言うものがあります。 鶴と亀が合わせて35匹いました。足の数は合計で94本あるとき、それぞれ何匹いますか?



鶴亀算 和算ナビ
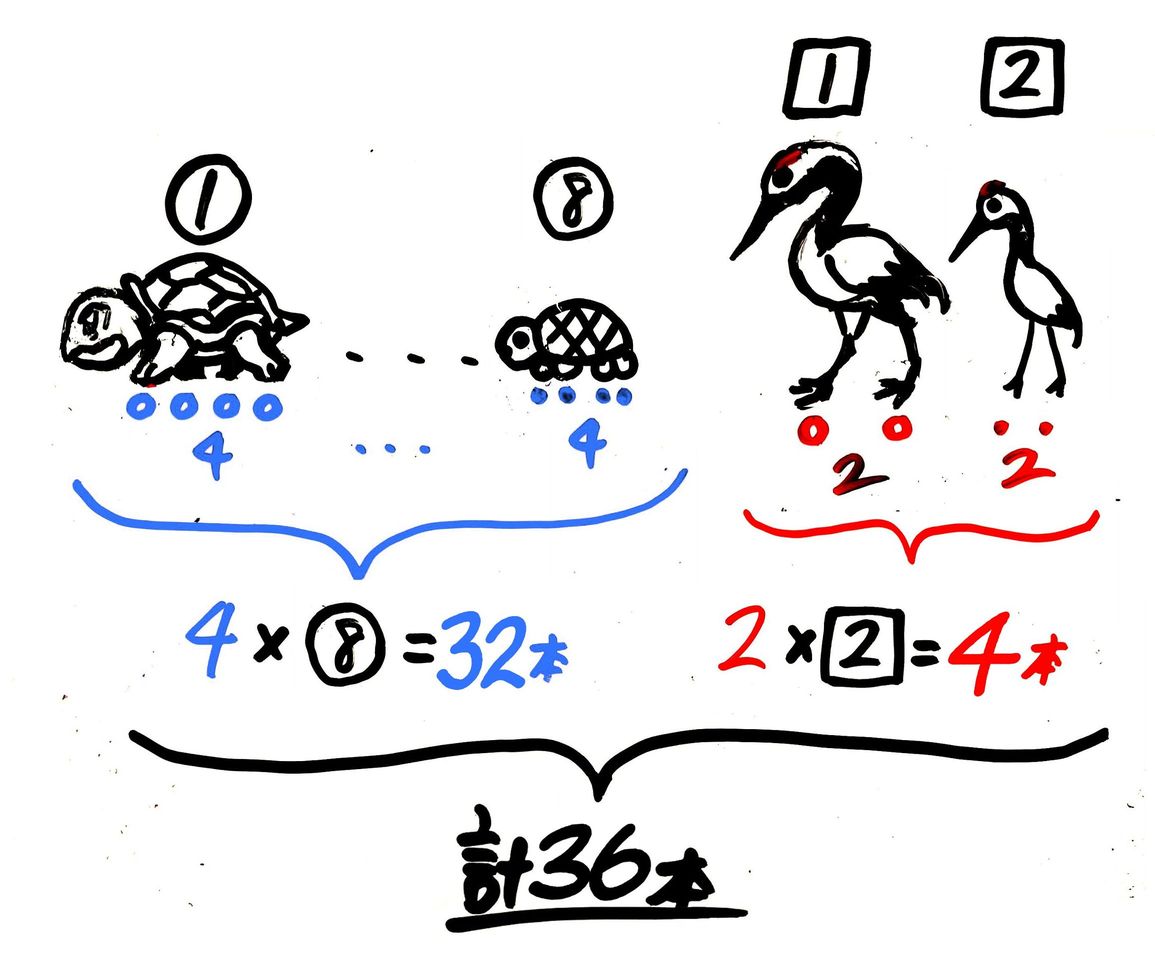



中学受験 つるかめ算とは 問題と解き方を分かりやすく図解 小学生 そうちゃ式 受験算数 新1号館 数論 特殊算
鶴亀算の原形・初出 中国 1299年 算学啓蒙 朱世傑 鶏と兎 中国では散逸。朝鮮に伝わる *注 中国 1593 年 算法統崇 程 大位 雉と兎 算術的解法 日本 1640 年 因帰算歌 今村知商 雉と兎 算術的解法 日本 1810 年 算法点鼠指南録 坂部勇左衛門 鶴と亀 代数的解法も紹介 鶴亀算の初出「算学啓蒙」は元の数学者、朱世傑が大徳 3年(1299)年に著した書物ですが、中国で は失われ、朝鮮でのみ伝わっていました。 豊臣秀吉の朝鮮侵攻の際に我が国に略奪品 として持ち帰られた本が現存しています。 「算学啓蒙」は宋・元時代の方程式論を使っ 中学受験を控えた息子から算数の手助けを頼まれ、自信満々の父親。 「月夜の池に鶴と亀があわせて16匹いる。 脚を数えると44本。 鶴と亀は
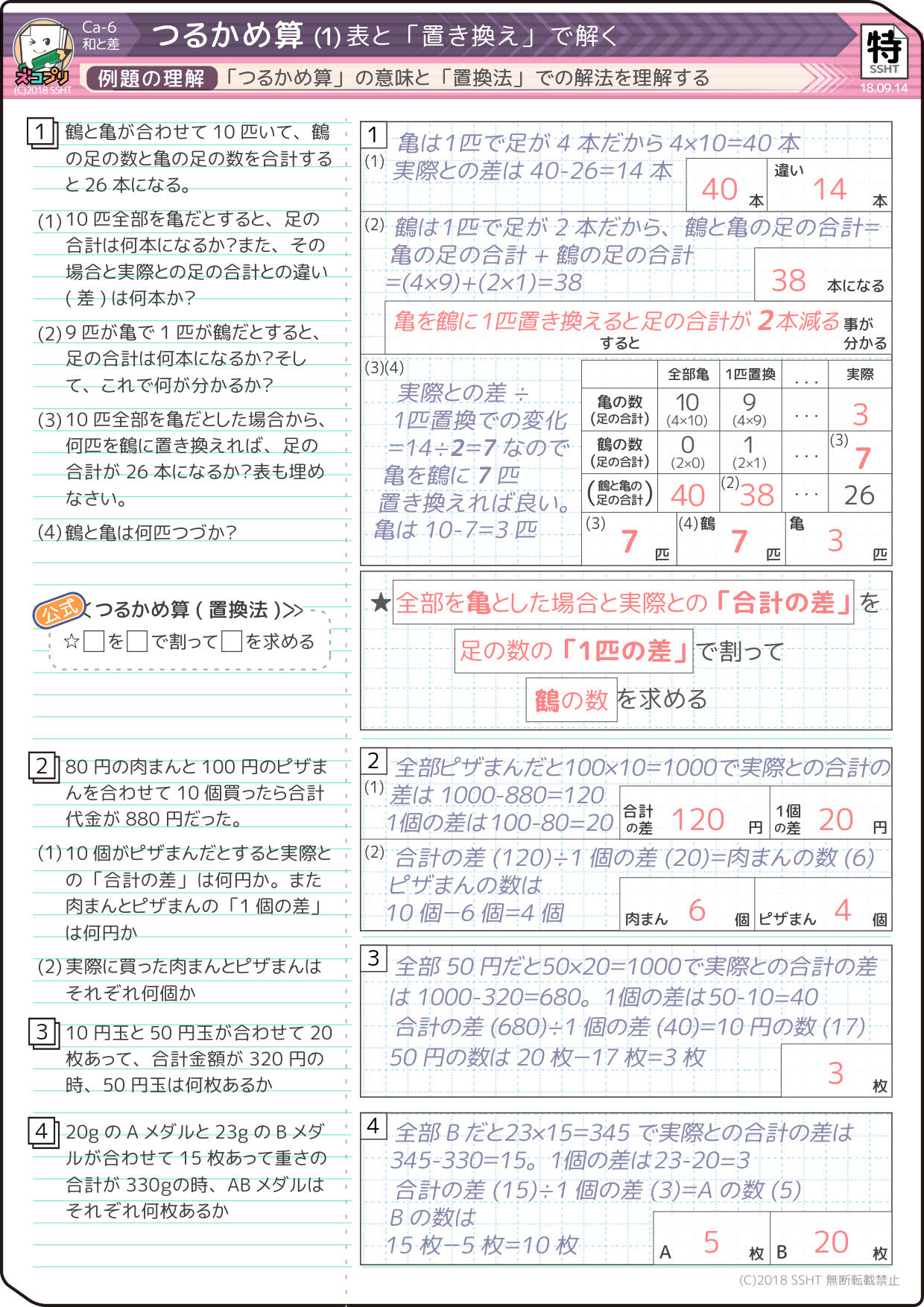



無料プリントあり 面積図を使わないつるかめ算の問題の解き方 置き換え法 小学生 そうちゃ式 受験算数 新1号館 数論 特殊算
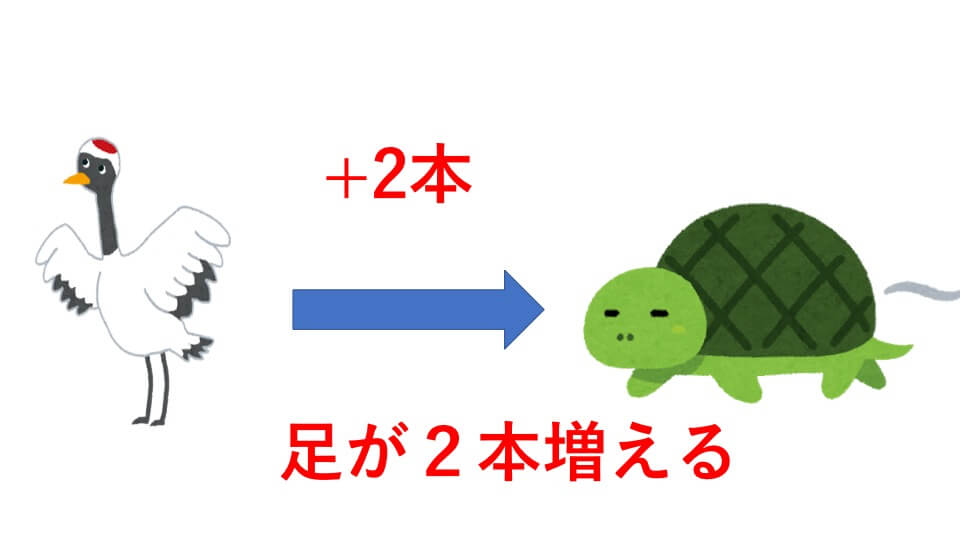



中学受験 算数 つるかめ算 表と面積図を利用して攻略 中学受験アンサー
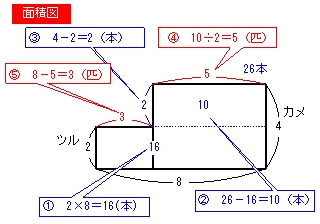
The "Tsurukamesan" 鶴亀算 in Japanese was changed animals, which are from pheasants and rabbits to cranes and tortoises This question is the solving method for firstdegree equation of two unknown numbers It, however, is not used algebraic method, is used the subjunctive method takehikom, "『鶴亀算(つるかめざん)は算数の文章題の典型問題または解き方の一種』" / minoru0707, "これ習ったかな?覚えてないな。 6×2 =12 6 匹すべてを鶴とすると、足は12 本。 -12 =8 足の数は合計で 本だから、8 本少ない。 8 ÷2 =4 亀を1 匹増やすと足の数が2 本増えるから、亀を4 匹増やせば、不足の8 本が解決! よって、亀は4 匹。



つるかめ算の解き方には 型 がある 中学受験プロ講師ぶろぐ



Spi M54e217p7lcis9d Com Turukame Nenrei Q6
江戸時代以前にわが国で独自に発達した数学のことを、西洋数学と対比させて和算と称しています。 明治以降、学校教育で西洋数学が教えられるようになると、日本固有の和算は表舞台から消えました。 しかし、和算は西洋数学と比べても、決して見劣りしない優れたものでした。 ねずみ算や鶴亀算など入門的な問題から、連立方程式、円周率、三角関数をはじめこの鶴亀算の理法を実際に起こりそうな事実に結びつけて 問題にすることは出来るが、どうしても不自然になり易く、必 要感若しくは実用性が稀薄になりがちである。 〔問題10:鶴亀算〕鶴と亀とが合わせて二十匹いる。足の数 は合計五十二本である。 鶴亀算で誰でも体感できる数学の「威力」と「限界」 問題2 12時間おきに1錠ずつ服用するようにともらった花粉症の薬がある。 この薬に含ま




算数文章題講座 つるかめ算の解き方 基本問題



ドリルズ 小学6年生 算数 の無料学習プリント鶴亀算 つるかめ算 基本
小学生の保護者の方にとっても、お子さんに算数を教える上でとても役立つ内容になっているので、ぜひ参考にしてみてください。 ※通常、鳥を数える単位は「羽」ですが、ここでは便宜上「匹」とします。 このような問題を「つるかめ算」と呼んでいます。 動物に限らず、50円切手と80円切手など商品とその値段が問題になっていることもあります鶴亀算は、 中学校 の 数学 における 連立方程式 の初歩的な問題にあたる。 一般的に、 x をツルの数、 y をカメの数、 a をツルとカメの個体数の総和、 b を足の本数の総和とおくと、 x y = a 2 x 4 y = b の2元1次連立方程式で表される。出典 フリー百科事典『ウィキペディア(Wikipedia)』 ( 0038 UTC 版) 鶴亀算 (つるかめざん)は 算数 の 文章題 の典型問題または解き方の一種。 小学生対象の問題として問われることが多いこともあり、通常は連立方程式を使わない解法を指す。 脚注 ^ " つるかめ算も濃度の問題も「面積図」で解ける 中学受験の算数のコツは、表を書き起こすこと




つるかめ算の歴史 愛知県名古屋市の学習塾 学習塾なら個別指導のキューブ 個別指導塾ピックアップ
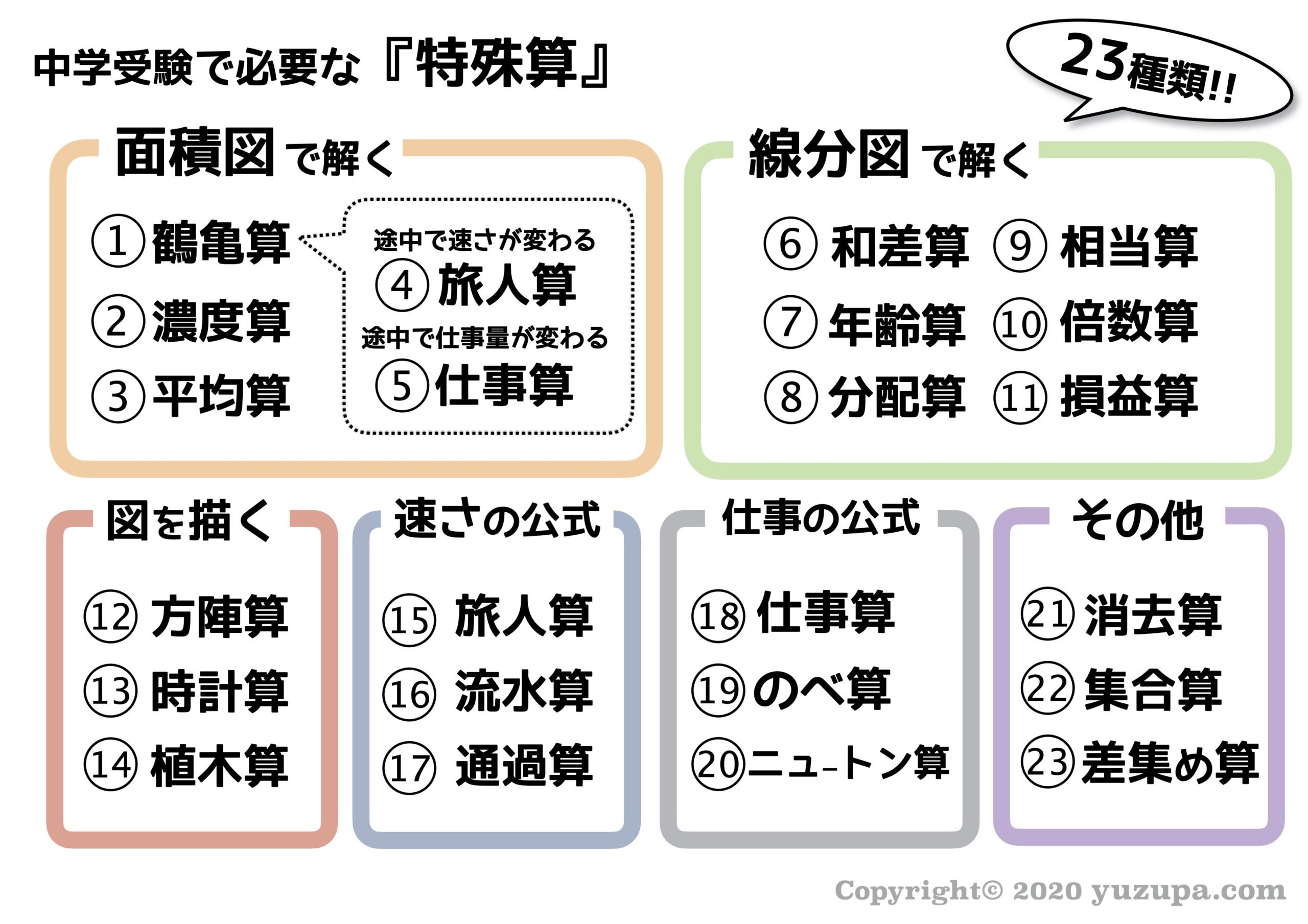



中学受験 特殊算は何種類ある 算数の文章題の見分け方 かるび勉強部屋
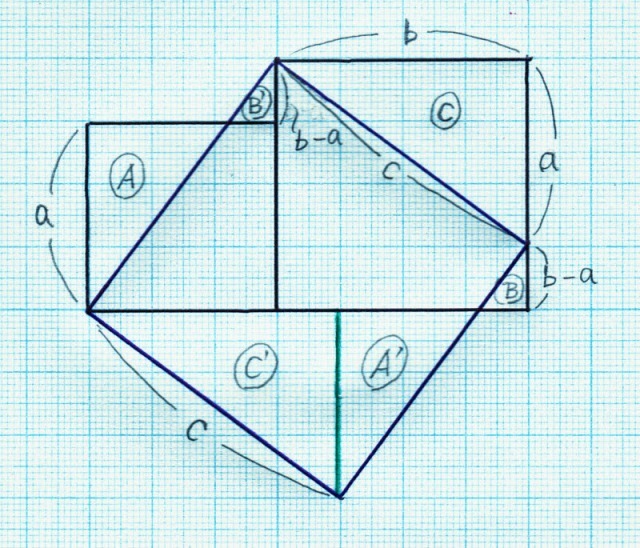



天声人語 鶴亀算の歩み を読んで 団塊世代高齢者の独白 兼吹上小学校同窓会ブログ




重要 のアイデア 62 件 中学受験 数学 勉強 算数
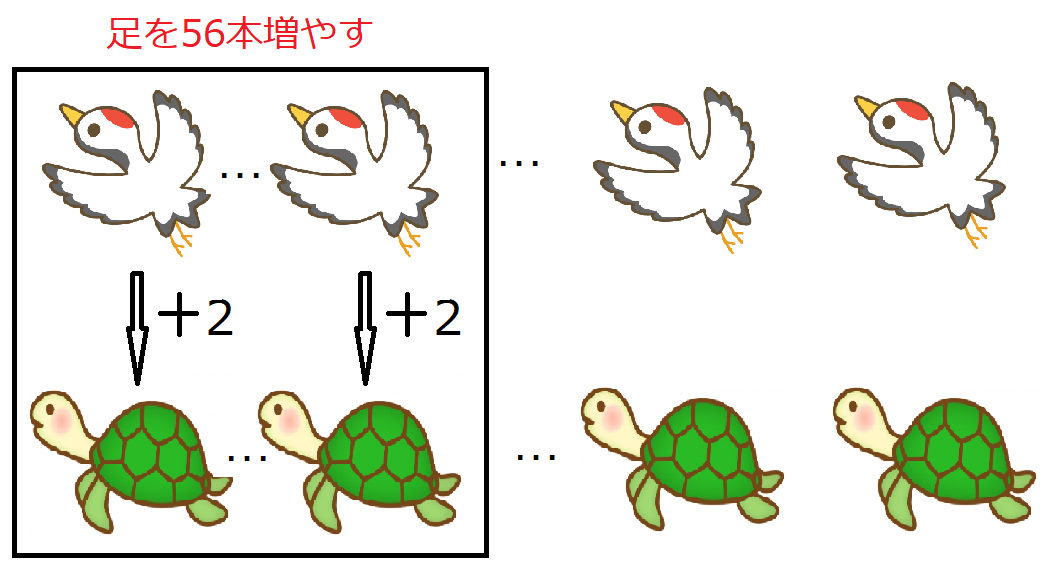



つるかめ算のわかりやすい解説 小学生 算数 公式 家庭教師のアルファ プロ講師による高品質指導



Osaka Kyoiku Ac Jp File Renkei Kenkyo Seika H28 2k 18 Pdf




覚えていますか鶴亀算 城西大学 城西大学 受験生サイト



ドリルズ 子供の無料学習プリント




楽天ブックス 江戸の算数 1 西田知己 本




古代中国数学 九章算術 を楽しむ本の通販 孫 栄健 紙の本 Honto本の通販ストア




中学受験 算数 つるかめ算 表と面積図を利用して攻略 中学受験アンサー
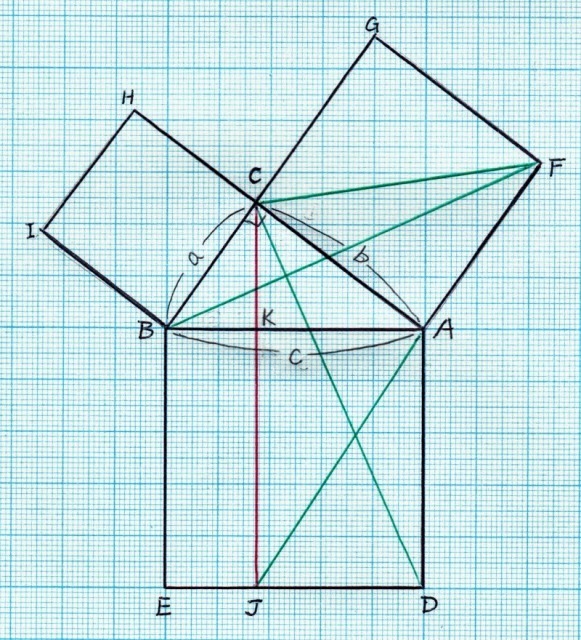



天声人語 鶴亀算の歩み を読んで 団塊世代高齢者の独白 兼吹上小学校同窓会ブログ
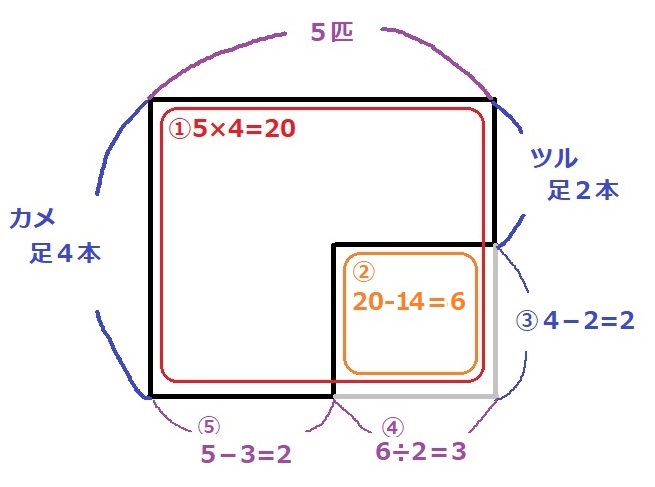



小1 鶴亀算 つるかめ算 を習得 爆走おてうブログ 中学受験25




小1 鶴亀算 つるかめ算 を習得 爆走おてうブログ 中学受験25




つるかめ算の歴史 愛知県名古屋市の学習塾 学習塾なら個別指導のキューブ 個別指導塾ピックアップ




鶴亀算 Wikipedia



C言語による鶴亀算 寝癖頭の解法




中学受験 特殊算は何種類ある 算数の文章題の見分け方 かるび勉強部屋 中学受験 小学校 算数 算数




小学生にもわかりやすい つるかめ算の解き方




小1 鶴亀算 つるかめ算 を習得 爆走おてうブログ 中学受験25




鶴亀算をどう解くか ー木村 亮 教授 株式会社 高知丸高



1




鶴亀算 たった2種類の公式と解き方のコツ 中学受験の算数 Yattoke 小 中学生の学習サイト




ヤフオク 江戸の数学教科書 桜井進 集英社インターナショ



中二数学激ムズ 孫子算経の問題で 鶴亀算 と言うもの Yahoo 知恵袋




つるかめ算の歴史 愛知県名古屋市の学習塾 学習塾なら個別指導のキューブ 個別指導塾ピックアップ



鶴亀算 もっと つるかめ算 算数 中学受験 文章問題




つるかめ算のわかりやすい解説 小学生 算数 公式 家庭教師のアルファ プロ講師による高品質指導




様々な教育課題への対応 19年度用 小学校算数 内容解説資料 大日本図書




ヤフオク 江戸の数学教科書 桜井進 集英社インターナショ



Http Www2 Ttcn Ne Jp Nagai Waseda Wasan Turu Pdf




Spi鶴亀算にまつわる由来とは 練習問題 解説有 日常生活つぶや記




和算 Instagram Posts Gramho Com




Spi鶴亀算にまつわる由来とは 練習問題 解説有 日常生活つぶや記



1



算数 仕事算 植木算 鶴亀算 小学生無料プリント 算数問題 国語問題 ドリル




小学生にもわかりやすい つるかめ算の解き方




中学入試まんが攻略bon 算数 つるかめ算 新装版 まんがではじめる中学入試対策 学研出版サイト




中学受験 特殊算は何種類ある 算数の文章題の見分け方 かるび勉強部屋 中学受験 勉強 算数




Spi鶴亀算にまつわる由来とは 練習問題 解説有 日常生活つぶや記



中学受験 特殊算は何種類ある 算数の文章題の見分け方 かるび勉強部屋



1




新小4 鶴亀算の解き方 面積図 連立方程式 1次関数 桜 戦記




中学受験 特殊算は何種類ある 算数の文章題の見分け方 中学受験 中学 勉強 算数



天声人語 鶴亀算の歩み を読んで 団塊世代高齢者の独白 兼吹上小学校同窓会ブログ



鶴亀算 和算ナビ




中学受験 特殊算は何種類ある 算数の文章題の見分け方 かるび勉強部屋 中学受験 中学数学 算数



鶴亀算 Wikiwand




ロイロノート スクール サポートページ 小6 算数 数学 和算に触れよう 鶴亀算 算数卒業旅行 授業案 洲本市立堺小学校 村上貴郎




つるかめ算の解き方解説5選 簡単でわかりやすい説明も



つるかめ算のわかりやすい解説 小学生 算数 公式 家庭教師のアルファ プロ講師による高品質指導




中学受験の基礎知識 つるかめ算1 Youtube



Http Www2 Ttcn Ne Jp Nagai Waseda Wasan Turu Pdf



Http Www2 Ttcn Ne Jp Nagai Waseda Wasan Turu Pdf




孫子算経 Wikipedia




和算の再発見 東洋で生まれたもう一つの数学 Dojin選書 城地茂 Hmv Books Online




鶴亀算の源流 雉と兎が同じ篭



鶴亀算 和算ナビ



ドリルズ 小学6年生 算数 の無料学習プリント 小6 鶴亀算 つるかめ算



つるかめ算 に 植木算 算数 特有の解法のはなし 日本最大級の編集プロダクション アーク コミュニケーションズ



Http Www2 Ttcn Ne Jp Nagai Waseda Wasan Turu Pdf



Ex08ans Prog0




鶴亀算と数学の調和 あのマス



ドリルズ 子供の無料学習プリント



中学受験 特殊算は何種類ある 算数の文章題の見分け方 かるび勉強部屋



Http Www2 Ttcn Ne Jp Nagai Waseda Wasan Turu Pdf



つるかめ算とは何 Weblio辞書




鶴亀算と数学の調和 あのマス




小学生にもわかりやすい つるかめ算の解き方
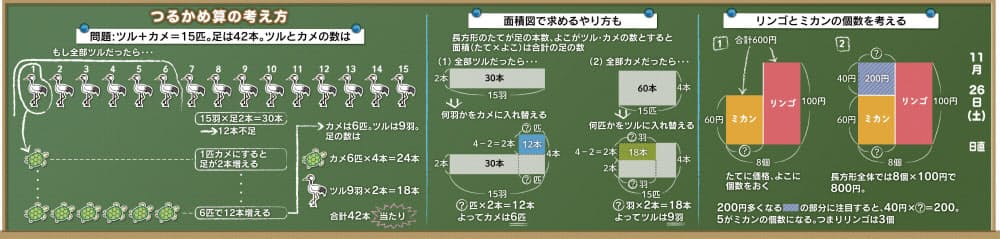



動物が出てくるつるかめ算のやり方を教えて Nikkei Style




つるかめ算の歴史 愛知県名古屋市の学習塾 学習塾なら個別指導のキューブ 個別指導塾ピックアップ




小学生にもわかりやすい つるかめ算の解き方



つるかめ算 に 植木算 算数 特有の解法のはなし 日本最大級の編集プロダクション アーク コミュニケーションズ



2



ドリルズ 子供の無料学習プリント




鶴亀算 たった2種類の公式と解き方のコツ 中学受験の算数 Yattoke 小 中学生の学習サイト



1



つるかめ算の解き方には 型 がある 中学受験プロ講師ぶろぐ




Sdgs史 0 方程式と鶴亀算 Oh 工学者 時々 哲学 Note




日本の数学 和算 わさん にチャレンジ 6年算数 津山瓦版



和算において 鶴亀算とは どういうものでしょうか Quora




小学生にもわかりやすい つるかめ算の解き方



ドリルズ 子供の無料学習プリント




小学生にもわかりやすい つるかめ算の解き方
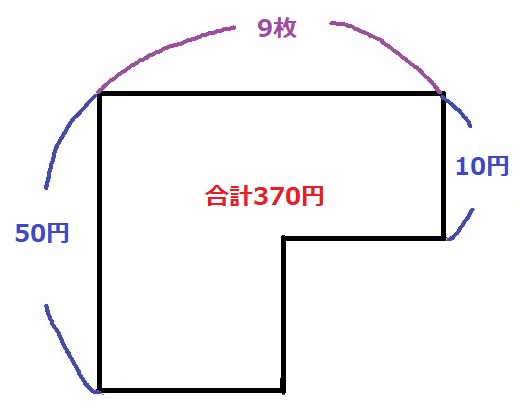



小1 鶴亀算 つるかめ算 を習得 爆走おてうブログ 中学受験25




โน ตของ Tnk S Note No 3 受験算数 M 鶴亀算 ช น Clear




中学受験の つるかめ算 の2つの解き方 面積図 表 数学fun




中学受験算数 割合のつるかめ算の問題 2つ割合の増減に注目 Stupedia




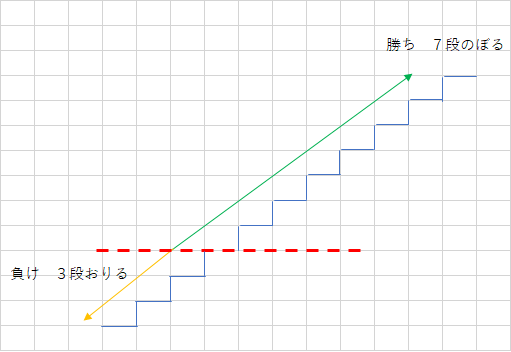
中学受験算数 3段つるかめを解く3つの方法




Sdgs史 0 方程式と鶴亀算 Oh 工学者 時々 哲学 Note




つるかめ算の歴史 愛知県名古屋市の学習塾 学習塾なら個別指導のキューブ 個別指導塾ピックアップ




割り算と鶴亀算 千寿の楽しい歴史 千寿の楽しい歴史



つるかめ算の解き方には 型 がある 中学受験プロ講師ぶろぐ




つるかめ算などの文章題の解き方 1 就活の為のspi非言語分野対策
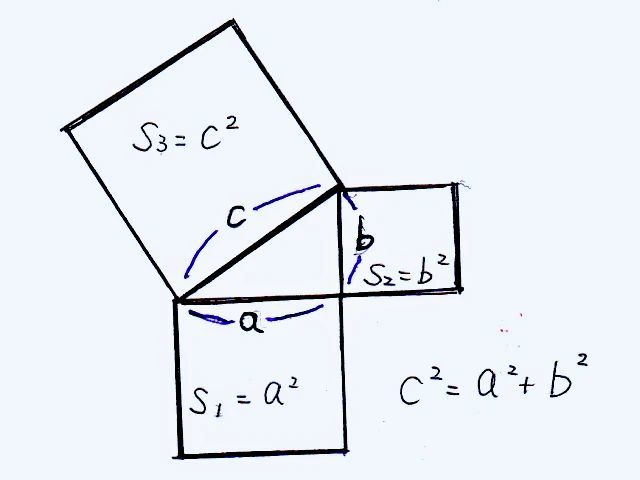



天声人語 鶴亀算の歩み を読んで 団塊世代高齢者の独白 兼吹上小学校同窓会ブログ




割り算と鶴亀算 千寿の楽しい歴史 千寿の楽しい歴史



0 件のコメント:
コメントを投稿