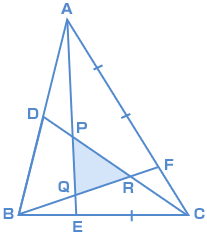
思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは,色々なタイプの図形問題を取り上げています。 図形ドリル 2つの直角三角形を組み合わせた図があります。色のついた三角形の面積は何cm2ですか。 PDFファイルをダウンロード思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは,色々なタイプの図形問題を取り上げています。 図形ドリル AB=AC,角BCD=90度の四角形ABCDがあります。三角形BCE,ADEの面積が24 cm2,9 cm2のとき,四角形ABCDの面積は何cm2で 今日は、中学受験で超頻出の「 正方形の中にある正方形の面積問題 」を紹介します。 親子で挑戦してみてください! 問題 図のように正方形の中にぴったり円が入っていて,その円の中にぴったりと正方形が入っています。

中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
三角形の面積 問題 中学受験
三角形の面積 問題 中学受験- 三角形の面積の公式―底辺×高さ÷2 三角形の面積の公式は 「底辺×高さ÷2」 です。 三角形の面積の求め方の3つのテクニック! 三角形の面積を求める問題は中学入試によく出ますが、 残念ながら単に公式に当てはめる問題はほぼありません。三角形ABCの面積が85c㎡のとき、三角形ADEの面積を求めなさい。ただし、辺BCは5等分されています。 → 解答 問題5 次の直角二等辺三角形の面積を求めなさい。 → 解答 問題6 面積が0c㎡の2つの正方形が、図のように重なっています。
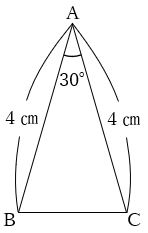



中学受験算数における15度と30度 中学受験プロ講師ブログ
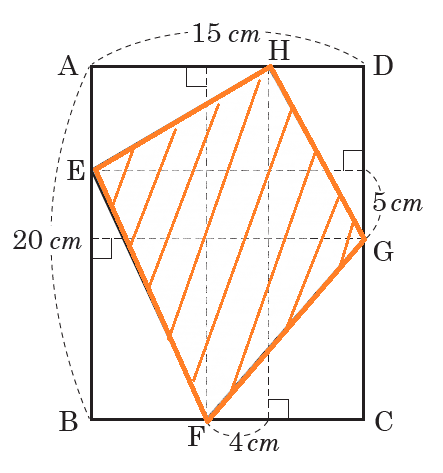
よって、三角形DHGの面積は135cm 2 。 DとE、GとFをそれぞれ結ぶ。 三角形DEHと三角形GHFの面積はそれぞれ 9cm 2 。 また、三角形DBE、三角形GFCもそれぞれ15cm 2 になる。 よって、台形DBCGの面積は6+135+9+9+15+15 =675cm 2 。 三角形ABCと三角形ADGの面積の比は1:4。 今日は、中学受験で超頻出の「 正方形の中にある正方形の面積 」問題を紹介します。 親子で挑戦してみてください! 問題 図のように正方形の中にぴったり円が入っていて,その円の中にぴったりと正方形が入っています。 問題1 三角形abcの辺abを2等分、辺bcを3等分、辺caを4等分し、点d、e、fを決めます。このとき、内部にできる三角形をpqrとします。また、cr : rp : pd=2 : 2 : 1、bq : qr : rf=2 : 2 : 1とします。
三角形、四角形の面積から、くふうして面積を求める問題です。 基本的な面積の求め方が分かっていれば解きやすい問題が多いので、よく出題されるパターンで練習して、確実に出来るようにしましょう。 よく出される問題 *色がついた部 ・三角形CDEの面積は96cm2 ・灰色部分の面積(?) ——————————– 図形の面積を求める問題ですね。 こちらも中学受験問題の定番です! この辺りも昔と変わっていませんね! 問題を読むと三角形CDEの面積は96cm2とあります。中学受験 算数の練習問題プリントです。栄光ゼミナールの約7万名の生徒が自宅や教室で毎日挑戦している問題データベースから、定番の問題を集めて公開しています。 中学受験 算数プリントの主な内容 和差算 植木算 周期算 分配算 方陣算 展開図と見取図 等差数列のしくみ 円と多角形 割合
図形問題が苦手といっても、そのタイプは様々。 今回は面積比の問題をサクッといきましょう! 目次 三角形の面積比で忘れちゃいけないこと 高さが同じで底辺の違いを見るだけ まとめ 三角形の面積比で忘れちゃいけないこと 面積比の問題で出てくる図形は、変な四角形だったり、四角形 したがって、三角形abeを図のように移動すると、 三角形aefは直角二等辺三角形です。よって、この面積を求めればよいので、 6×6÷2=18 より、四角形abedの面積は 18cm 2 (答)(2) 三角形gdeの面積は何cm2ですか。 (3) 四角形ghbeの面積は何cm2ですか。 相似の応用(偏差60近辺) 右の図の四角形abcdは正方形で,点p,qはそれぞれ辺bc, cdのまん中の点です。また,dpがaqとacと交わる点をそれぞれr,sとします。 (1) dr:rs:spを求めなさい。



中学入試で頻出 鎌倉学園の図形問題 横浜の学習塾 国大qゼミ



面積比と長さ比 東京都市大学付属中学 2012年 長さ比 面積比 どう解く 中学受験算数
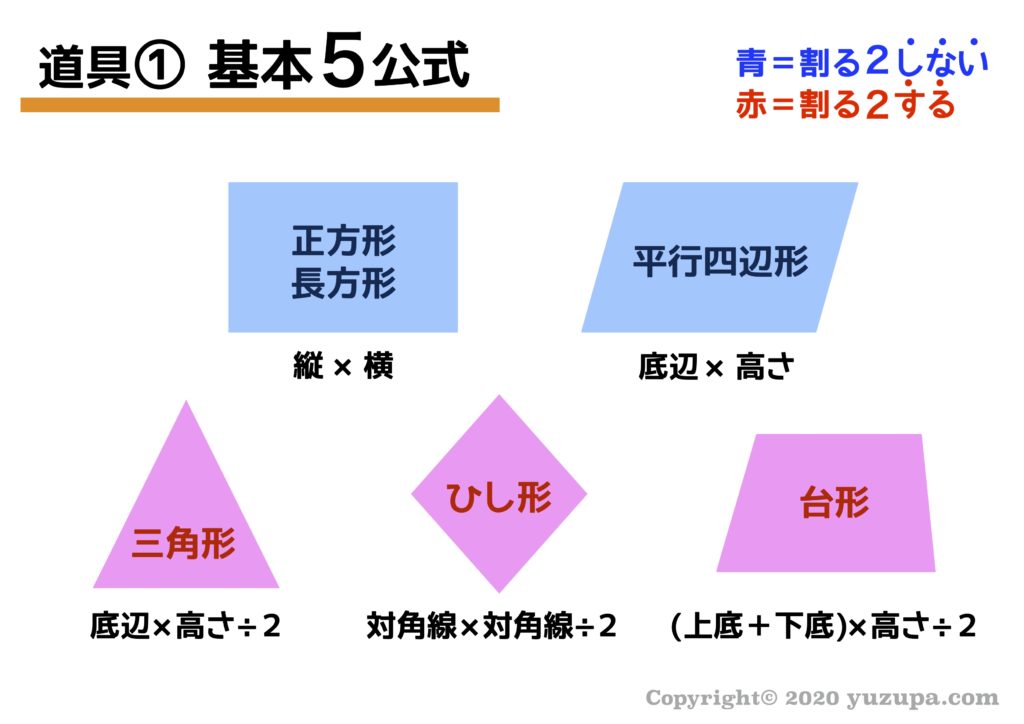
正方形の面積は三角形の面積の何倍?(15年 渋谷教育学園幕張中学) ABCと pqrの面積比は?(豊島岡女子学園中学 12年) ;三角形と四角形の面積の求め方を覚えましょう。 三角形の面積=底辺×高さ÷2 ※ 「高さ」がどの部分の長さなのかをていねいに考えて下さい。 長方形の面積=たて×よこ 正方形の面積=1辺×1辺 平行四辺形の面積=底辺×高さ ひし形の面積=対角線×これにより、円の面積は、12×314=3768c㎡ よって、図の黒くぬった部分の面積は、 3768c㎡24c㎡=1368c㎡ (答え) 1368c㎡ (参考) この問題や練習問題6のような場合、正方形と円の面積の比は、1:157です。 ← 問題に戻る 次の問題 →



1




面積 3 図形問題 算数 正方形 中学受験 高校受験 勉強 Youtube スタディチューブ
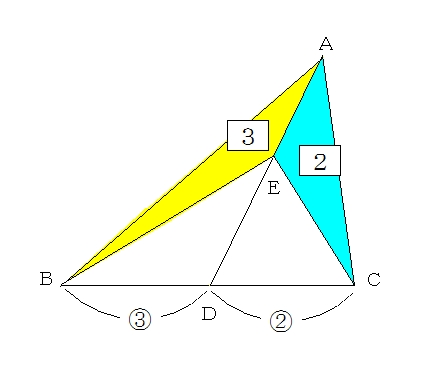
右の図の三角形abcにおいて、bd:dc=1:2です。三角形dceの面積が三角形abcの面積の半分になるとき、ae:ecを求めなさい。 定番問題というよりは、 2辺の比から面積の比を求める基本問題の逆算パターンです。 「隣辺比」 と呼ばれる解き方です。 右の図の中学受験算数 図形のマジック 057倍と157倍 1木の葉形 右の図の木の葉形の面積は正方形の面積の057倍です。 ただし,円周率が314のときしか使えません。 右の図では,10 10 057 = 57(cm2)とな正三角形と半円(灘中学 受験算数問題より) 木の葉形面積とヒポクラテスの三日月 牛の動く範囲の面積(sapixディリーサポートより) 正方形と円(SAPIX入室、組分けテストより) 補助線と面積(芝中学 受験算数問題 09年)



辺の比と面積比




平面図形をマスター 三角形の面積比 応用編その3
円とおうぎ形のいろいろな面積の問題です。 学習のポイント 正方形とおうぎ形を合わせた形の面積を素早く求められるようにしましょう。 *色のついた部分の面積を求めます。 4分の1のおうぎ形2つから正方形をひく、4分の1のおう 正三角形と面積比の問題です。 正三角形と1度がからんでいるので、正三角形の「方眼紙」を利用して解きます。 詳しくは、灘中学校19年算数1日目第9問の解答・解説で。 正三角形の「方眼紙」を利用して解く問題は、麻布中学校などで出題されています。 こんばんは~ つつです。 今日は、中学受験向けの算数の問題を一緒にやってみましょう! 難関私立中学を受験するなら知っていなくてはダメです。 特に算数の図形の問題は、受験の合否に直結します。 もちろん受験が終わった後にも活用できる内容になっています。 三角形の面積を弧



面積比 長さ比 これが中学入試に出た図形問題



平面図形の問題 中学受験 田中貴 Com
中学受験 図形について学習していきましょう。 取り上げるのは受験算数でも出題頻度(ひんど)の高い「面積と角度」です。 最初は難(むずか)しく感じるかもしれませんが、まずは基本的な問題で解き方・考え方をしっかり定着させましょう。 そうどこを見ればいい!? どこが高さ!? 三角形が2つくっついている!? 面積応用問題; 受験生がまちがえやすい問題やポイントをもっと学習したい方は、本書をご購入ください。 算数図形編 でる度⇒ ★★★ 《面積・線分の長さ》 四角形を直角に注目して分けよう




三角形で面積比と底辺の比の関係は 平面図形分野の頻出問題を考える みみずく戦略室
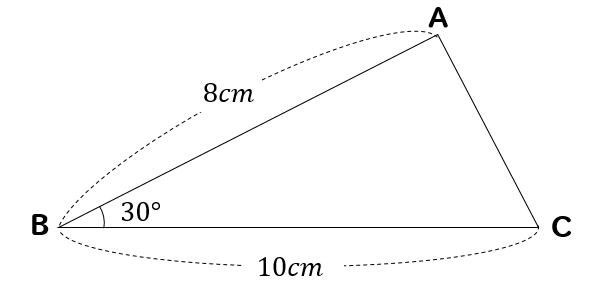



小学算数 30度の三角形ってどうやって面積求める 辺の比は 数スタ
四谷大塚予習シリーズ算数の手書き解説です。 四谷大塚 予習シリーズ のテキストは四谷大塚よりお買い求め下さい。 著作権は中学受験の算数・理科ヘクトパスカルに帰属します。転載または、商用での無断使用を禁止します。 予習シリーズ手書き解説のコース名と価格表 予習シリーズ手書き東海中学の問題と同じように、問題図に重ねてみると、 三角形(赤)の面積=3 とすると 高さが等しいので、 三角形11の面積=1 三角形8の面積=2 です。 また、正八角形の面積=3×8=24 ですから、 三角形9と三角形10の面積の和=12-(2+1+3)=6 です。頂角が等しい二つの三角形の面積比 b apq abc = ap×aq ab×ac 8 斜めに置かれた三角形の面積公式 b abc=l×h× 1 2 9 台形上の上底と下底に平行な線分の長さ b pq= × × 10 中線定理 d ab2ac2=2(am2bm2) 11 内接円を利用した三角形の面積 b



中学受験 図形の面積問題は 7つ道具 で攻略 かるび勉強部屋



東京 男女御三家 の算数問題を解く 21年中学入試 後編 中学受験への道 ダイヤモンド オンライン



中学受験 図形の面積問題は 7つ道具 で攻略 かるび勉強部屋



最高 50 正三角形 面積 求め方




中学受験の円に関する問題 角度 長さ 面積の基本問題まとめ 算数数学苦手克服 家庭教師のマスコンサルティング
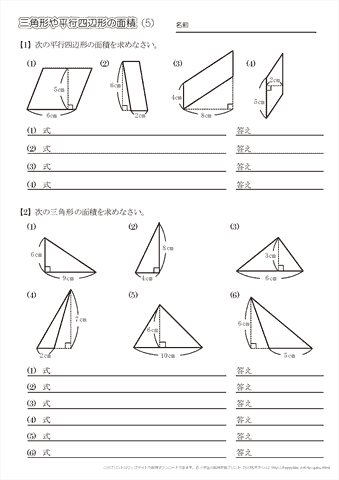



小学5年生の算数 三角形や平行四辺形の面積 問題プリント ちびむすドリル 小学生




中学校入試問題 算数 解いてください 半径9cmの円 を4分の1 に Okwave




面積 11 図形問題 算数 四角形の面積 城北中学校 中学受験 Youtube




平面図形をマスター 三角形の面積比 応用編その3



平面図形の面積 第19問 面積比 市川中学 05年 平成17年度 受験算数問題 まいにち一題 中学受験過去問題研究




中学受験算数における15度と30度 中学受験プロ講師ブログ
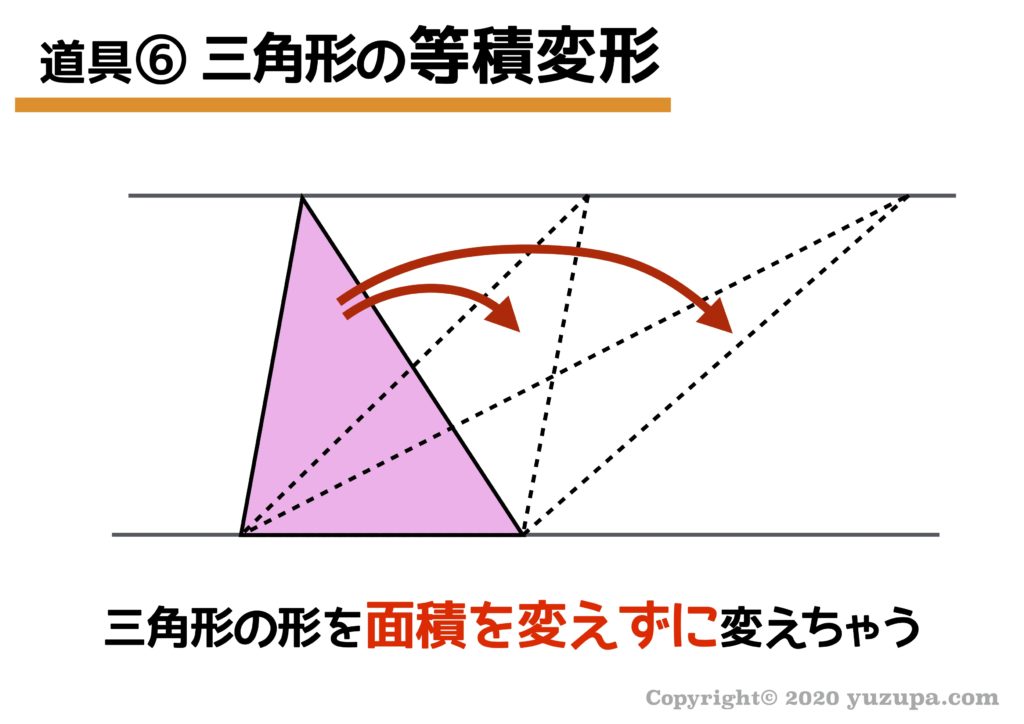



中学受験 図形の面積問題は 7つ道具 で攻略 かるび勉強部屋




中学受験算数 三角形の2辺の比と面積比の問題 Stupedia
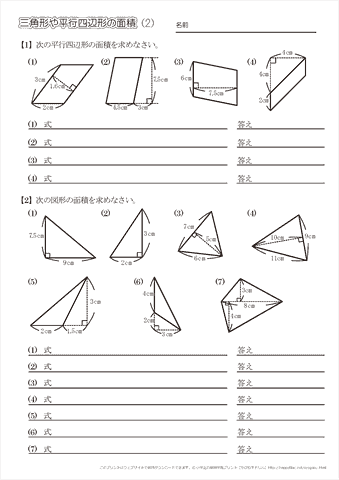



小学5年生の算数 三角形や平行四辺形の面積 問題プリント ちびむすドリル 小学生




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




平面図形をマスター 三角形の面積比 応用編その3
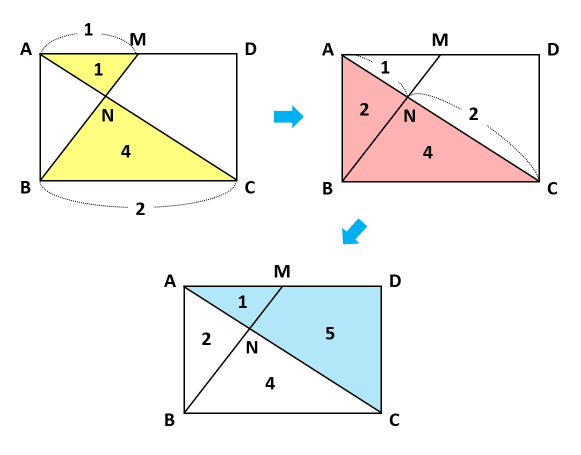



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ
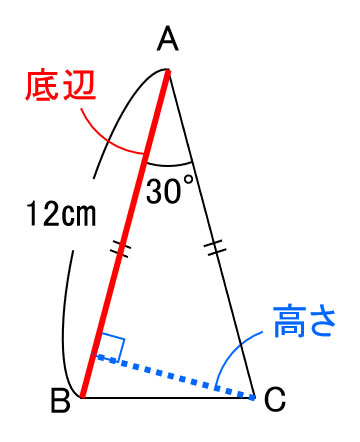



中学受験算数のちょ 怪しい三角形 中学受験プロ講師ブログ
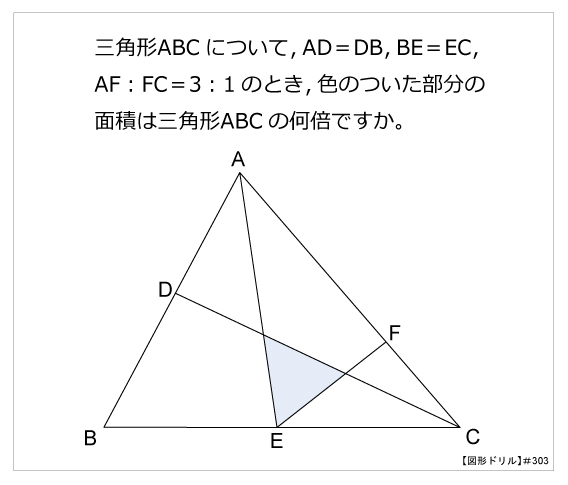



図形ドリル 第303問 三角形の面積比 算数星人のweb問題集 中学受験算数の問題に挑戦




合同 算数星人のweb問題集 中学受験算数の問題に挑戦
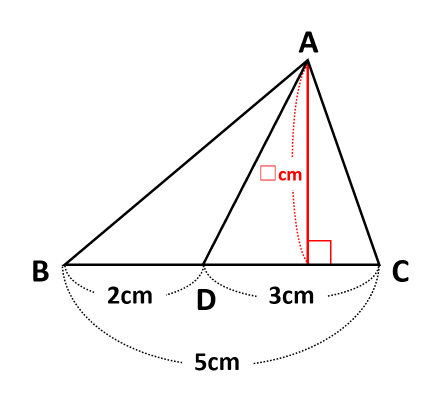



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ




補助線の引き方 日々の学習 兄中学受験




小学6年生 算数 10月 辺の比と面積の比 速さ 1 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ




楽天ブックス 中学受験算数 面積比の達人 みかん 本
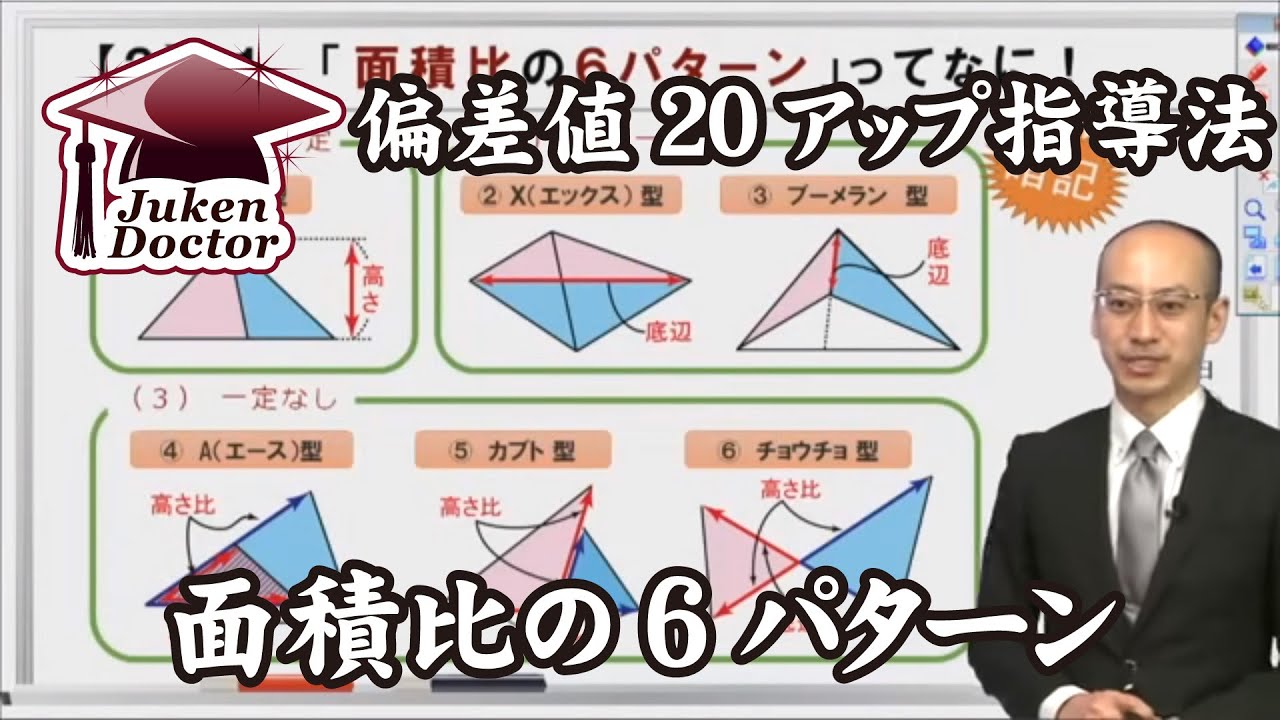



8 面積比の6パターン って 中学受験ドクター Youtube




神戸女学院中2018年 面積ー 中学受験算数の良問 難問 基本問題
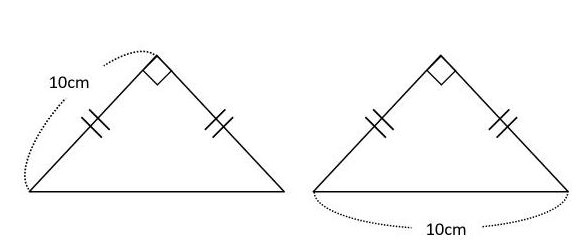



三角形の面積 中学受験 塾なし の勉強法
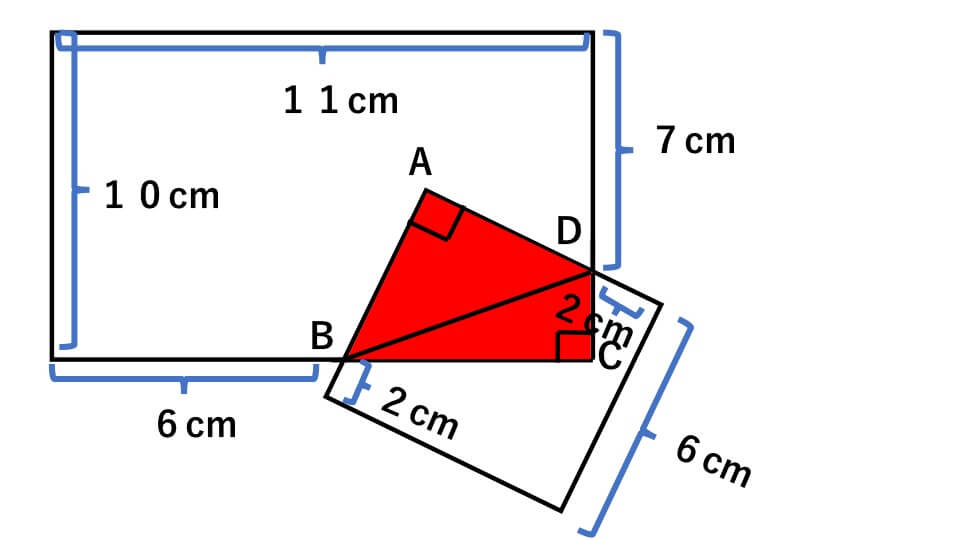



中学受験 算数 面積 よく出る応用問題や難問をわかりやすく解説 中学受験アンサー




灘中2019年 面積ー 中学受験算数の良問 難問 基本問題
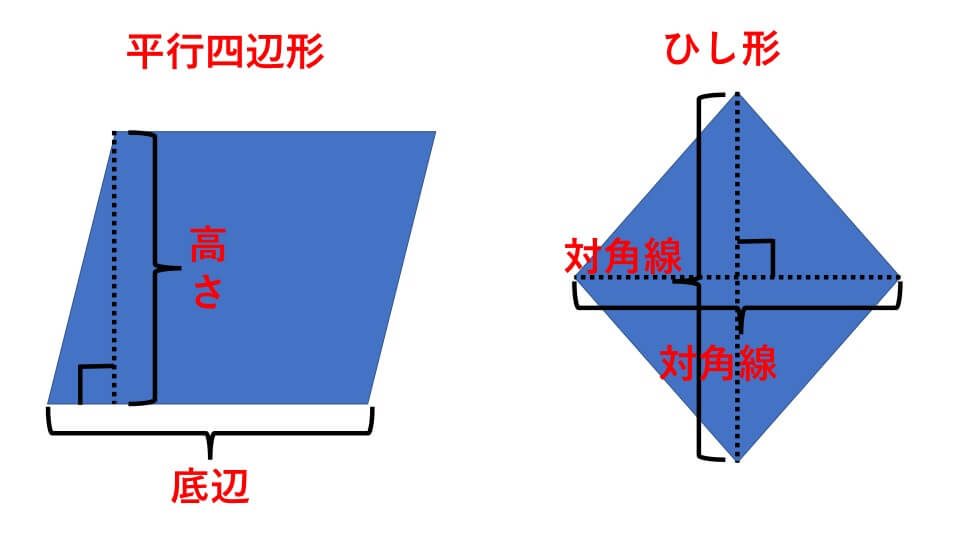



中学受験 算数 面積 よく出る応用問題や難問をわかりやすく解説 中学受験アンサー
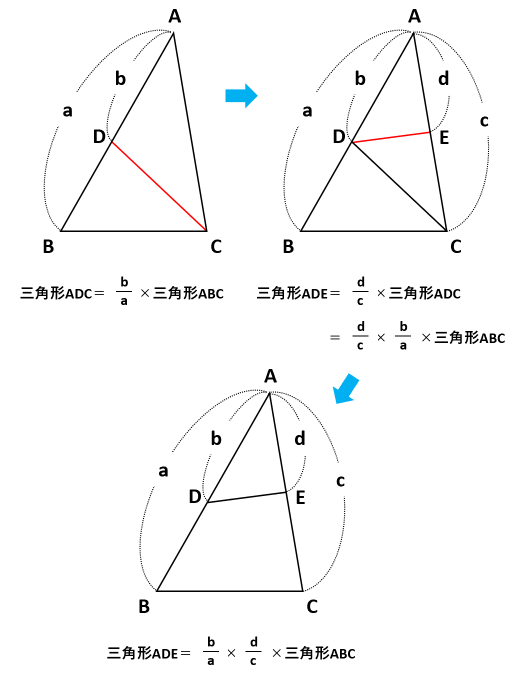



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ




小6ハイレベル算数 正三角形と面積比 中学受験 中学入試 Youtube




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




ヤフオク 算数 難関私立中学受験 高校受験対策に 革命的
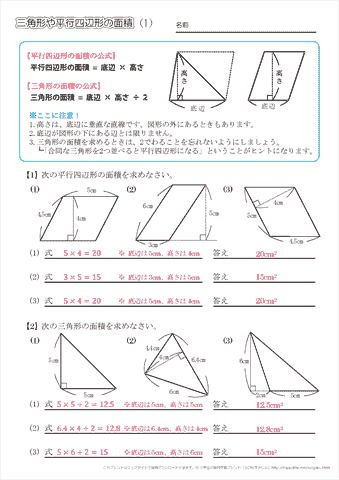



小学5年生の算数 三角形や平行四辺形の面積 問題プリント ちびむすドリル 小学生
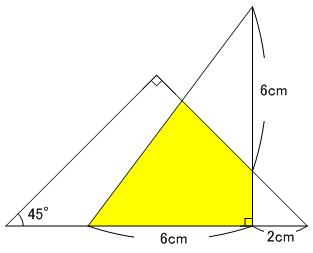



三角形が重なった部分の面積 栄光学園中学 05年 中学入試算数問題解けるかな
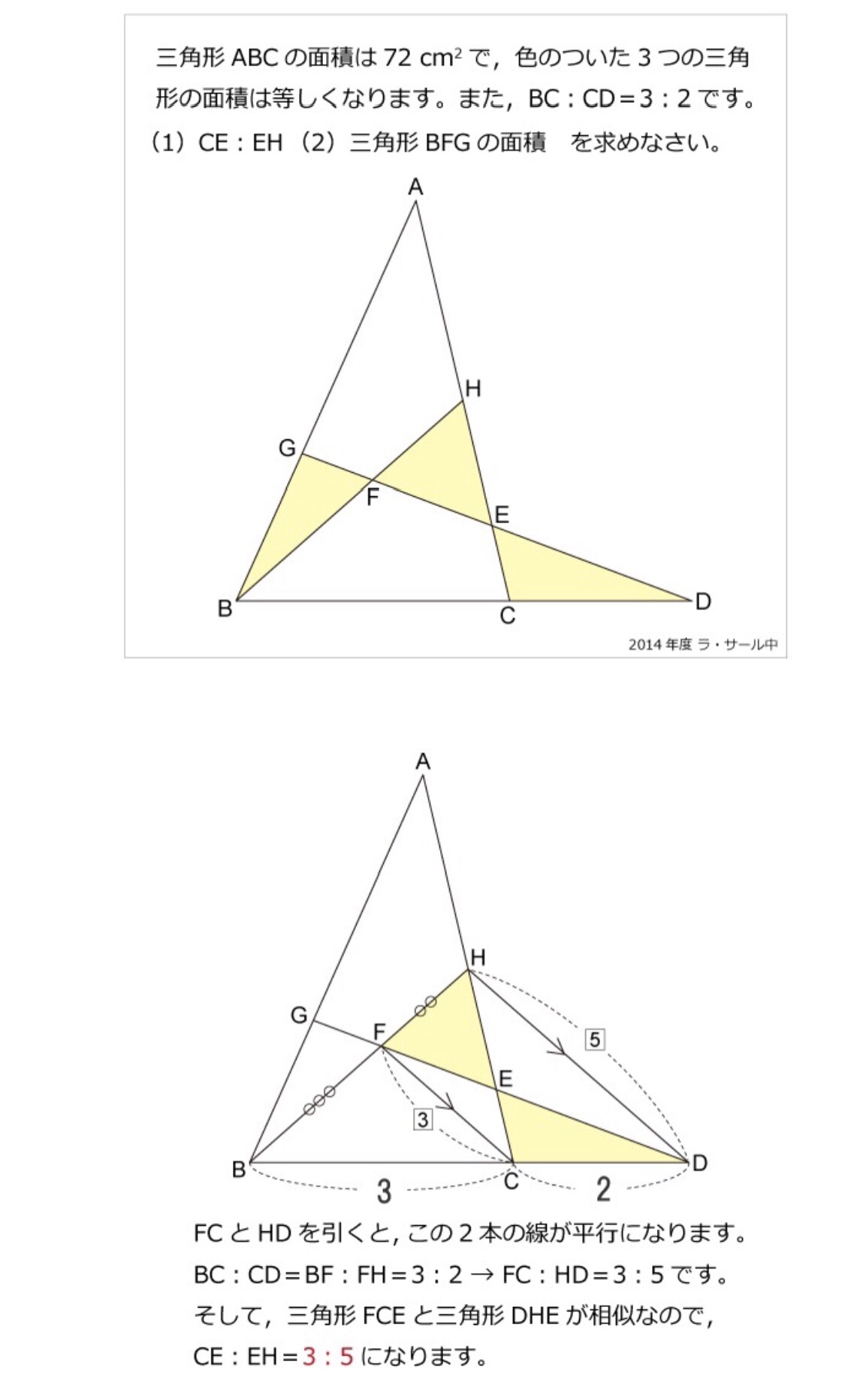



補助線の引き方 日々の学習 兄中学受験
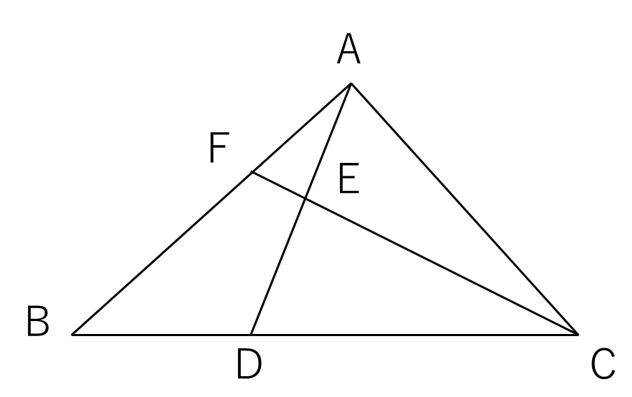



三角形の面積比をてんびんで解く 中学受験プロ講師ブログ




平面図形が苦手な人は必見 三角形の面積比と辺の比の関係 基礎編
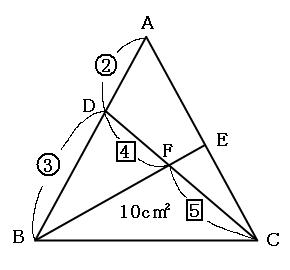



面積と辺の比の関係を解説 図形の面積と辺の比の関係はテントやドリルで面積を求める




よく出る台形の面積比 算数 過去問で基本を鍛える 12 勉強法のバイブル 帝都大学へのビジョン



正三角形と半円 灘中学 受験算数問題より どう解く 中学受験算数




中学受験 苦手な 図形 で得点力アップ 学習の秘訣は ポチたま中学受験




平面図形をマスター 三角形の面積比 応用編その2



1




中学受験 算数 三角形の面積比は底辺探すだけでok 補習塾ぬまーの寺小屋
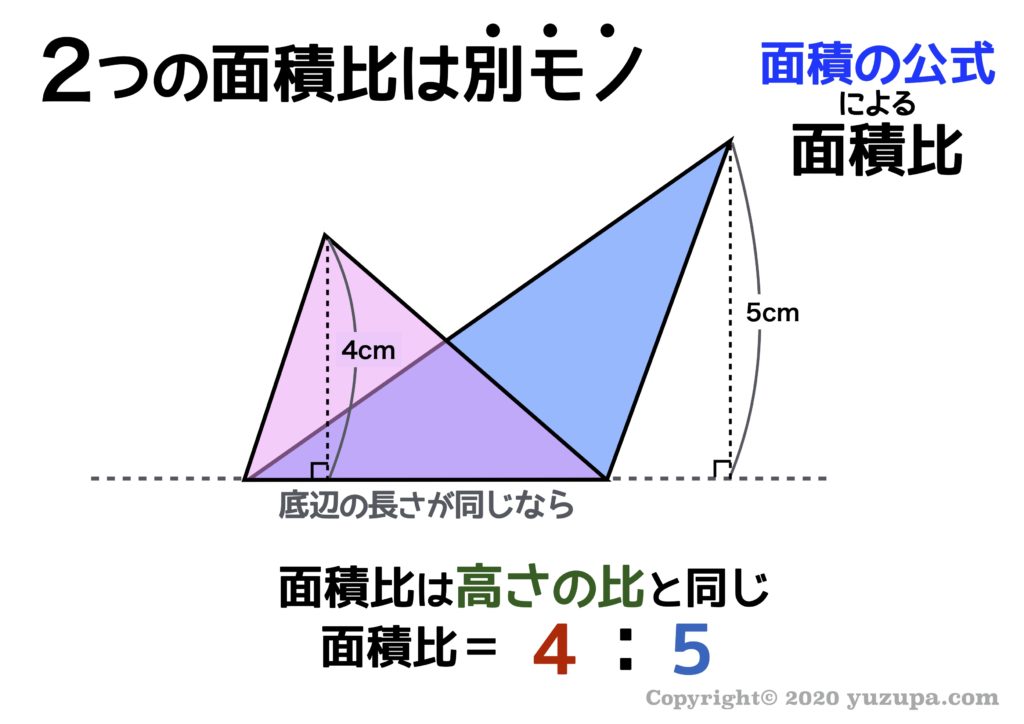



中学受験 図形の面積問題は 7つ道具 で攻略 かるび勉強部屋
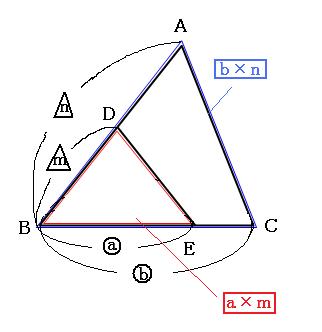



面積と辺の比の関係を解説 図形の面積と辺の比の関係はテントやドリルで面積を求める



1
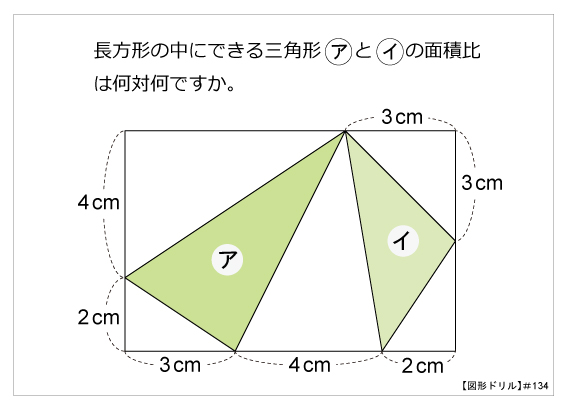



図形ドリル 第134問 三角形の面積比 算数星人のweb問題集 中学受験算数の問題に挑戦




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



算数 平面図形と比 1 中学受験 ベネッセ教育情報サイト



面積 これが中学入試に出た図形問題




中学受験 算数 面積 よく出る応用問題や難問をわかりやすく解説 中学受験アンサー
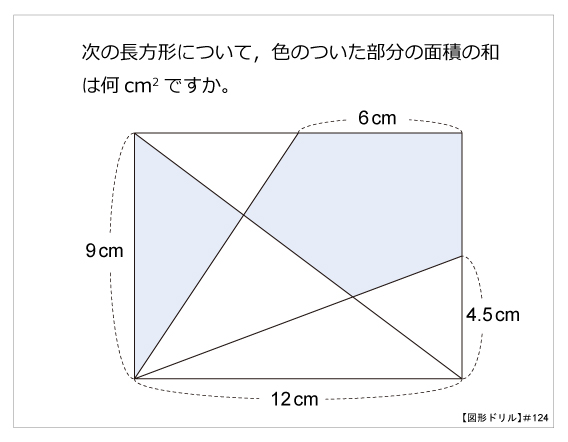



図形ドリル 第124問 長方形と面積の和 算数星人のweb問題集 中学受験算数の問題に挑戦
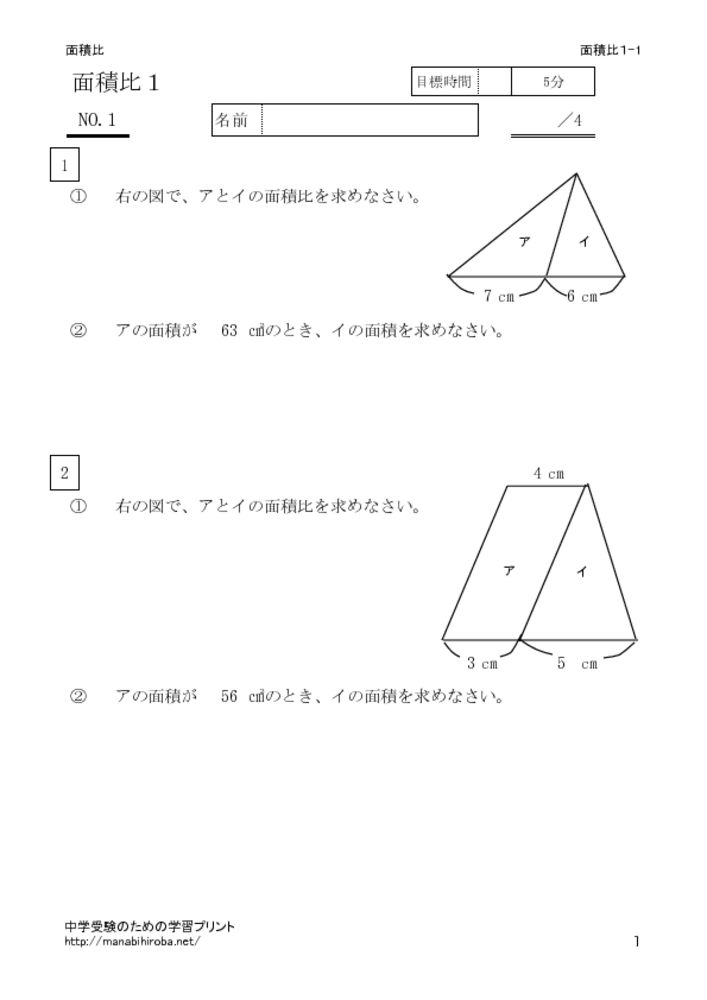



面積比の基本 中学受験準備のための学習ドリル




超頻出 正三角形の中にある正三角形の面積 問題 恋する中学受験 大学受験を見据えた中学受験




面白い算数の問題 円 面積 算数 中学入試 Youtube




中学受験 年 灘中算数入試問題1日目第8問目 三角形と内接する正方形の面積を推理して 解説 おまけあり 中学入試 Youtube
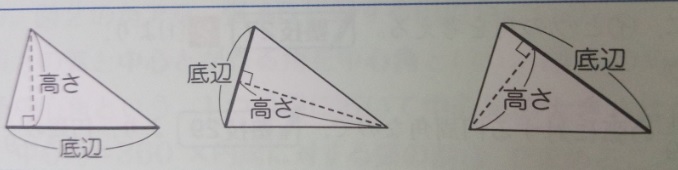



三角形の面積 中学受験 塾なし の勉強法




中学受験向け 三角形の面積を弧の長さから求める方法と なぜそうなるのか 効率厨 オレ の考えた最強の中学受験ブログ




平面図形をマスター 三角形の面積比 応用編その2




中学受験 算数 三角形の面積比は底辺探すだけでok 補習塾ぬまーの寺小屋




平面図形をマスター 三角形の面積比 応用編その2
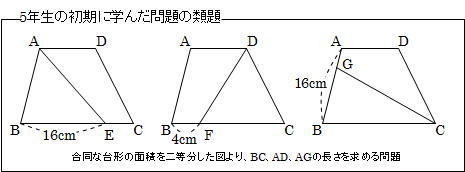



小5の学習ポイント4 辺の比と面積比 前田昌宏の中学受験が楽しくなる算数塾
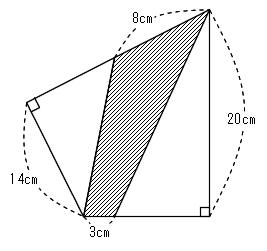



図形の面積問題を得意にする6つのチェック 効果的な勉強方法は 前田昌宏の中学受験が楽しくなる算数塾




年度中学入試 平面図形の最難問 東大カリスマ塾長 浜田一志公式ブログ 9割が伸びる 文武両道 勉強法



面積比を求める問題 慶應義塾中等部 2010年 どう解く 中学受験算数




算数図形編 面積 線分の長さ 四角形を直角に注目して分けよう 中学受験 高校受験パスナビ



三石 数学塾 2017中学入試 算数
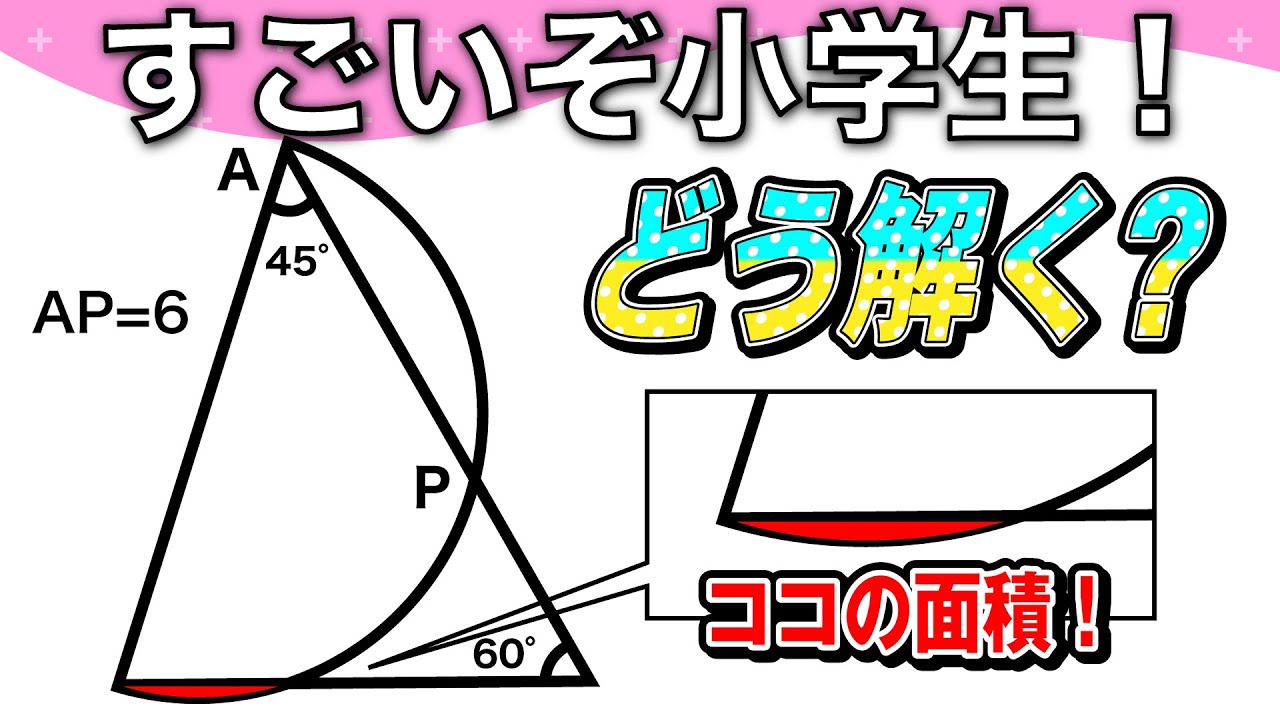



面白い算数問題 中学受験 中学入試 算数 解説 成蹊中学 平面図形 Youtube



算数の図形問題に特化した中学受験対策問題集 算数図形マスター シリーズ 新発売 数研出版株式会社のプレスリリース




中学受験の算数 面積の問題 わからないので教えてください よろしくお願い Okwave



中学受験 図形の面積問題は 7つ道具 で攻略 かるび勉強部屋



六甲中学入試問題 2009年 算数4番 三角形の面積 正方形 正三角形 30度問題




辺の比と面積 平面図形 中学受験の算数 理科ヘクトパスカル




算数図形編 面積 線分の長さ 対称な図形を追加してみよう 中学受験 高校受験パスナビ



面積比 長さ比 中学受験ー算数解き方ポータル




大妻 三角形の面積の差 ジーニアス 中学受験専門塾
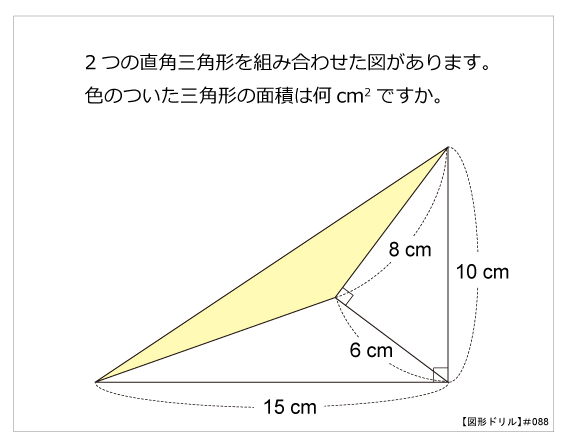



図形ドリル 第問 直角三角形と面積 算数星人のweb問題集 中学受験算数の問題に挑戦
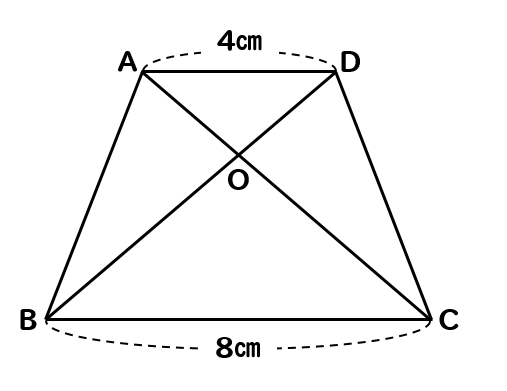



相似 台形と面積比の問題を徹底解説 数スタ
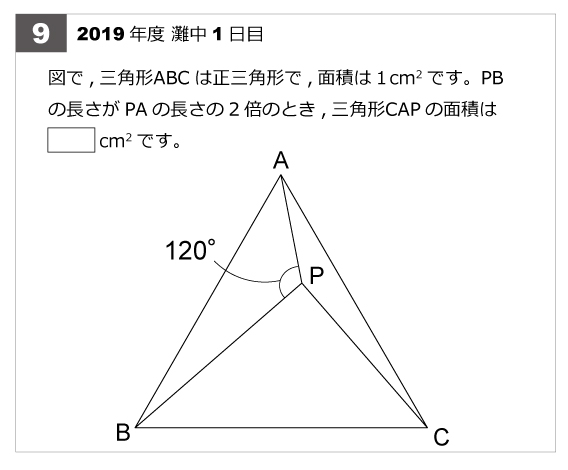



灘中解説速報 19年第9問 正三角形と面積比 算数星人のweb問題集 中学受験算数の問題に挑戦




平面図形をマスター 三角形の面積比 応用編その2



中学受験 算数の問題です 三角形abcと三角形bdeの面積は等し Yahoo 知恵袋




高槻中学入試問題 過去問を何回かやると力がつけられそう 現役進学塾プロ講師による中学受験算数実践オンライン講座




脳トレにも使える中学受験算数 図形問題編 中学受験算数を解く Vimagic Books 株式会社ヴィーマジック 大曲 隆毅 数学 Kindleストア Amazon



中学受験 算数数学が苦手な子専門のプロ家庭教師みかん先生
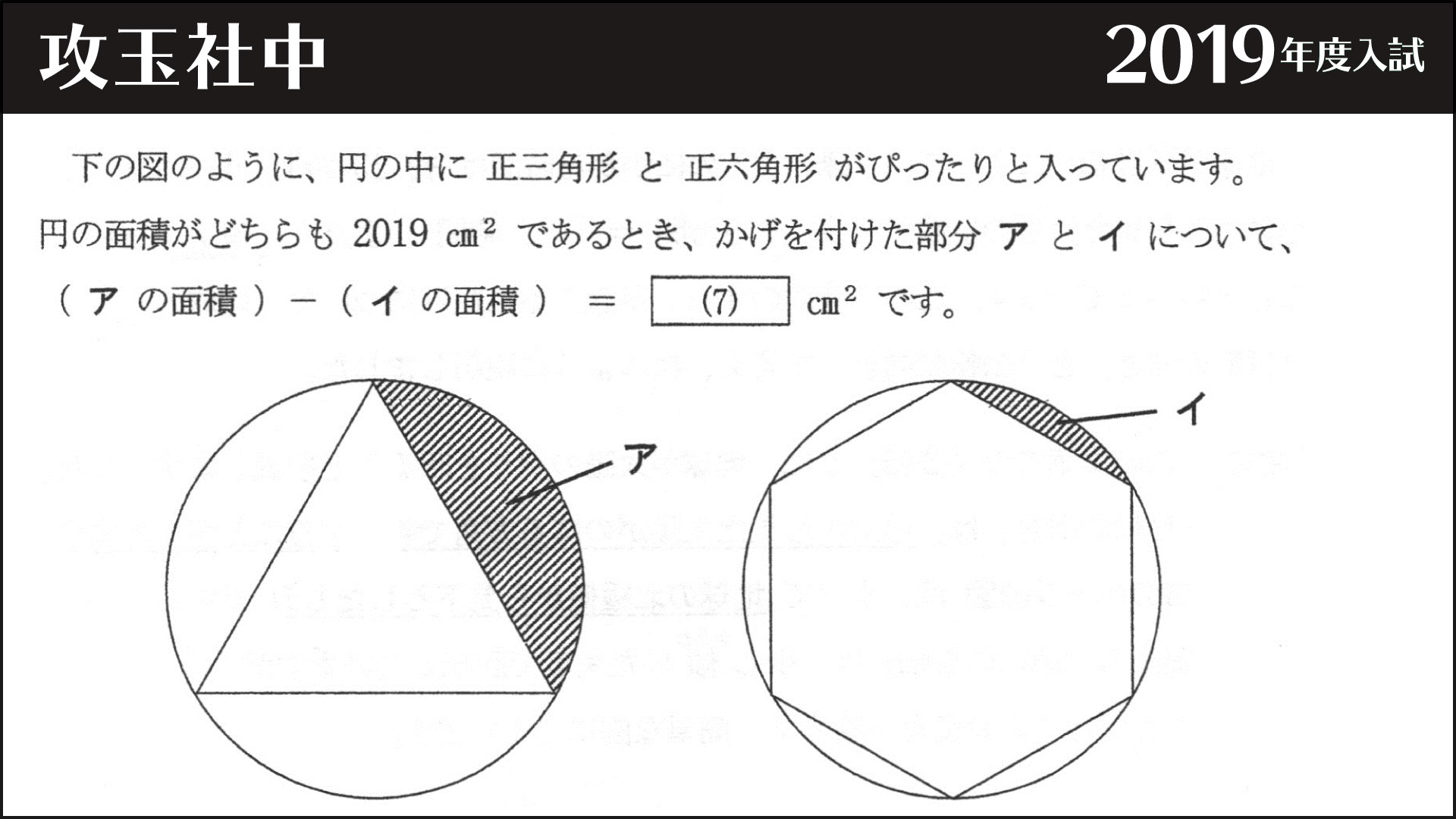



攻玉社 正六角形と正三角形と扇形の面積 ジーニアス 中学受験専門塾



しょうちゃん 公式ブログ 算数の問題を解いてみる その13 図形 Powered By Line



1



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生



Newみんなの算数講座86 三角形を全部見てはいけない 中学受験の算数知恵宝庫
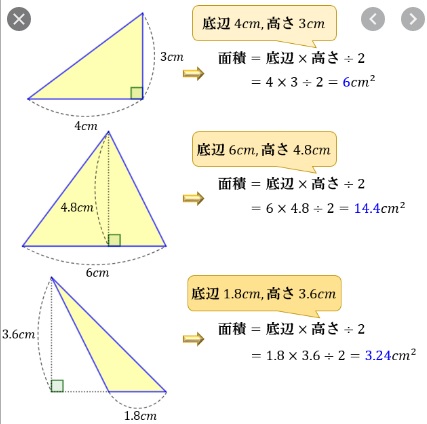



三角形の面積 中学受験 塾なし の勉強法



中学受験の算数の問題です 問題 下の図のように辺bcの長さが5 Yahoo 知恵袋



0 件のコメント:
コメントを投稿